Understanding the Basics of Structural Reliability
Structural reliability is a crucial concept in engineering that deals with the estimation of a structure’s safety level under uncertainty. Unlike deterministic approaches that provide single numbers with no variation, structural reliability focuses on probabilities, reflecting real-world uncertainties in material properties, loads, and other factors. Just think about it, if your load rating factor for a bridge girder is 0.99, does that really mean that your girder has/will fail? Therefore, a probabilistic approach allows for a more comprehensive understanding of safety and performance, which is particularly relevant in the context of rare events, with probabilities of failure ranging between 10 − 2 and 10 − 8.
The Three Pillars of Structural Reliability
Structural reliability estimation is structured around three core steps:
- Identifying Limit States: These are conditions under which a structure no longer meets its performance requirements. This is akin to defining a failure event in probabilistic terms. The reliability is calculated for a proposed failure mechanism, i.e. a limit state.
- Determining Governing Variables: Every limit state is influenced by certain variables, both in terms of the structure’s capacity (resistance) and the demands (loads) placed upon it. Identifying these and their probability distributions is key.
- Calculating the Reliability Index: This index quantifies the reliability index or the probability of failure, incorporating the uncertainties identified in the previous steps.
The heart of structural reliability is the limit state function, g(X), where X represents the set of design variables (both resistance and load variables). A structure is deemed to fail when g(X) ≤ 0.
Probability of Failure: A Closer Look
To quantify the probability of failure, we look at the probability that the limit state function falls below zero. Mathematically, this is expressed as:
Pf = ℙ(g(X) ≤ 0)
Mathematically, this can also be calculated by integrating the probability density function of G over the failure domain.
Methodologies for Estimating Pf
Estimating the probability of failure (Pf) can be approached through:
- Analytical Methods: Used when exact solutions are available, particularly for linear combinations of Gaussian load and resistance.
- Approximation Methods: Including first-order reliability methods (FORM) and second-order reliability methods (SORM), these are used when exact solutions are infeasible, focusing instead on approximating the limit state function near critical points.
- Simulation Methods: Techniques like Monte Carlo simulation provide accurate estimates for Pf by sampling design variables, especially useful for highly nonlinear limit state functions or when computational resources allow.
Case Study: Simple Problem with G = R − S
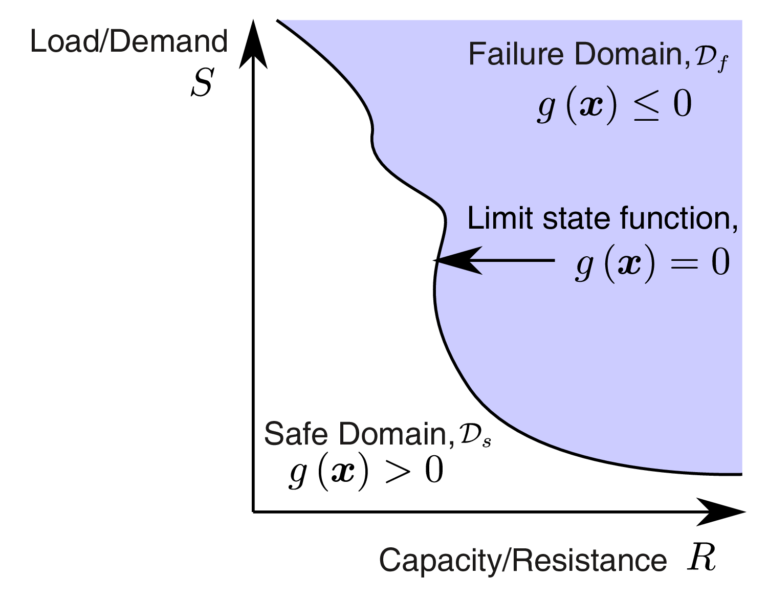
Consider a basic structural reliability problem where the limit state function is defined as G = R − S, with R representing resistance and S the load. For example, considering the ultimate bending limit state for a simply supported beam, R would represent the resistance of the beam and S would represent the bending moment on the beam for a given set of loads. The probability of failure arises from the overlap between the probabilities of these two variables. For example, let us visualize the entire domain of R and S in a 2D plot. The limit state function G = 0 represents the boundary between safety and failure, i.e. when R is exactly equal to S. This boundary partitions the domain of all possible values of R and S into two regions: safe region (where R>S) and a failure region, R ≤ S. The probability of failure of the structure, Pf, is the ratio of the failure domain to the entire domain of R and S. The reliability index β is a proxy measure for Pf, which is estimated after doing certain transformations of the domain of R and S. There are multiple advantages of estimating the reliability index over directly estimating Pf. These are covered in a separate post.
Conclusion
Structural reliability melds the precision of engineering with the probabilistic insights of data science, providing a robust framework for assessing structural safety under uncertainty. By embracing this approach, engineers and data scientists alike can better quantify and mitigate risks, ensuring structures that are not only resilient but also optimally designed to withstand the unpredictable.
Note: For deeper dives into structural reliability, seminal texts like Nowak’s 2000 book on the subject provide extensive frameworks and methodologies.