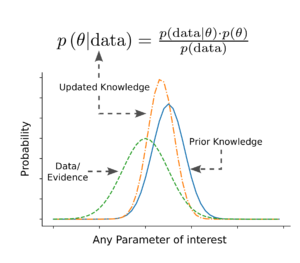
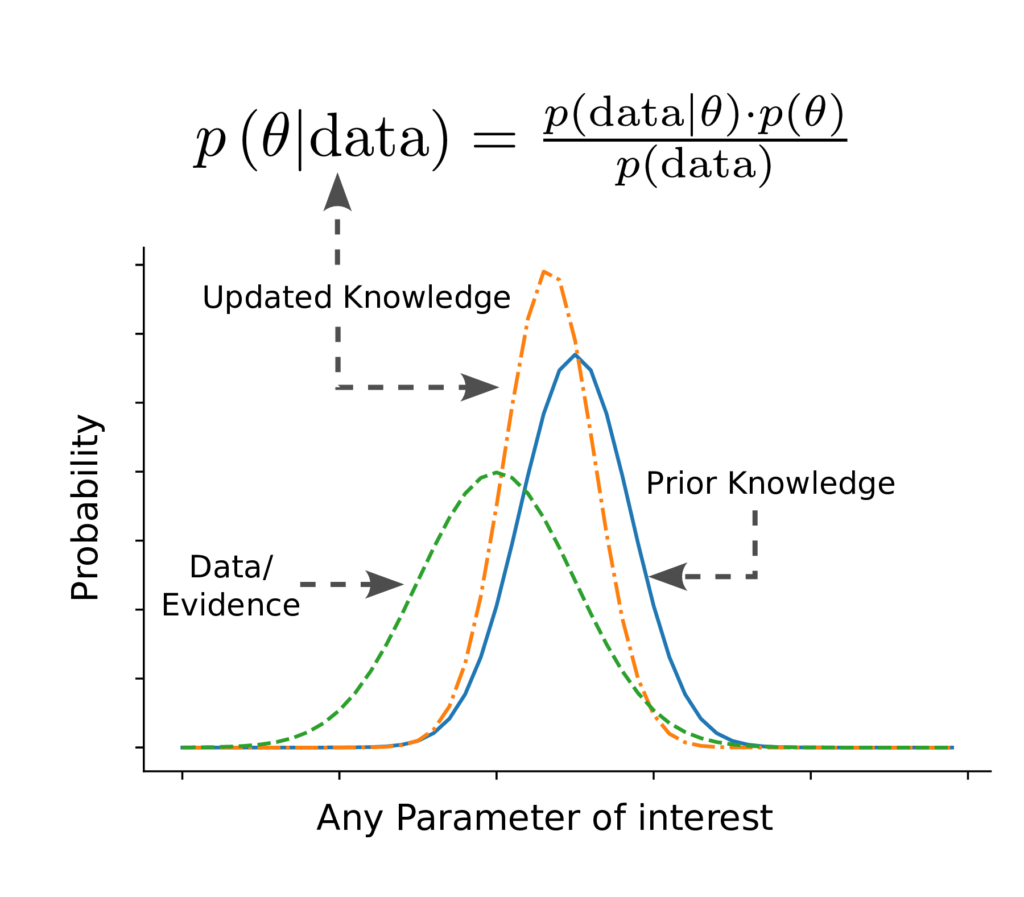
Bayesian statistics offers a powerful framework for updating beliefs based on new evidence, a concept rooted in the foundational theorem by Thomas Bayes. This approach is particularly valuable in data science for refining models and making informed decisions. Let’s delve into the key mathematical concepts and the philosophy behind Bayesian updating, and explore its advantages over the frequentist methodologies commonly used in statistical analysis.
Understanding Bayesian Updating
At the heart of Bayesian statistics is the concept of updating our knowledge about the world with new evidence. Suppose we have a set of parameters governing structural performance, denoted by , with a joint probability density function (PDF) given by
. When we obtain new measurements of these parameters, denoted by
, we can “update” our knowledge or distribution of
, resulting in an “updated” or posterior distribution,
.
Mathematically, this is represented as:
where is the likelihood function representing the probability of observing the measurement
for a given value of
,
is the prior distribution, and
is the posterior distribution. The Bayes rule can also be simplified by considering only the terms that depend on
, where
is a normalizing constant:
Likelihood Function: Bridging Data with Theory
The likelihood function is a cornerstone in Bayesian updating, representing how probable our observed measurements are, given the model parameters. It is not a probability distribution itself but a function that assigns probabilities to different possible values of the parameters based on the observed data. Whether dealing with binary outcomes (e.g., whether a structure is safe or failed) or continuous measurements (e.g., the size of a crack), the likelihood function shapes our updated beliefs.
Bayesian Updating in Action: An Example
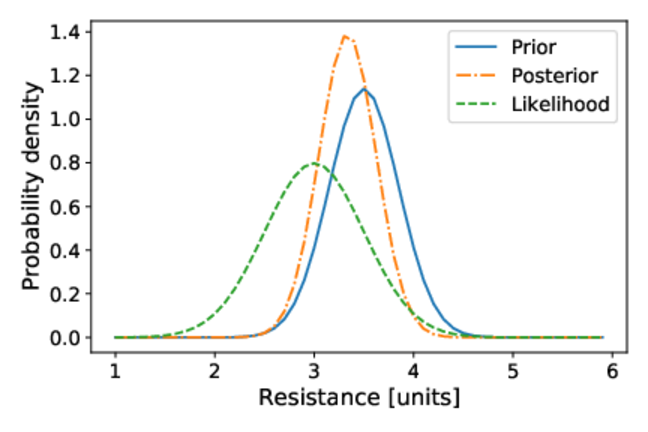
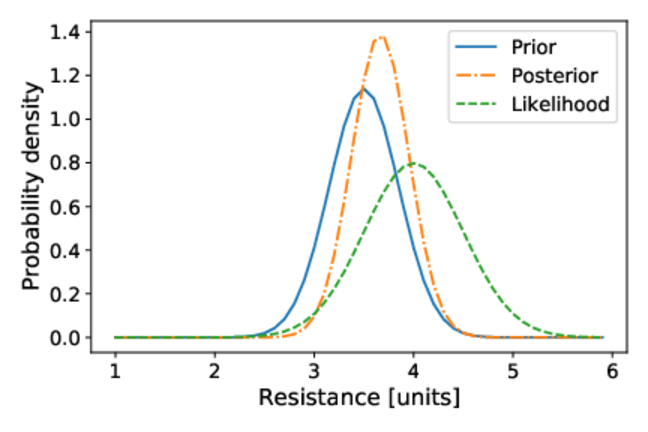
Consider the resistance of a hypothetical structural component that is normally distributed, , where the mean is 3.5 units and the standard deviation is 0.35 units. If the measurement’s accuracy is 0.5 units, the likelihood function for observing a measurement
when the resistance is
can be modeled as a normal distribution,
.
Through Bayesian updating, the effect of new measurements (e.g., 3.0 units or 4.0 units) on our beliefs about the resistance’s value is illustrated by shifts in the posterior distribution towards these measured values.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Advantages of Bayesian Updating Over Frequentist Methodologies
Bayesian updating offers several advantages:
- Integration of Prior Knowledge: It allows the integration of prior knowledge or beliefs into the statistical analysis, which is particularly useful in fields where past information is valuable.
- Flexibility in Model Updating: As new data becomes available, Bayesian methods provide a systematic way to update predictions or models, reflecting the latest information.
- Handling of Uncertainty: Bayesian approaches provide a probabilistic framework for dealing with uncertainty, offering a more nuanced understanding than point estimates or binary decisions.
Methodologies for Posterior Distribution Estimation
In practice, determining the posterior distribution can be straightforward if the prior and likelihood follow specific distributions, known as conjugate distributions. However, when they do not, computational methods like Markov Chain Monte Carlo (MCMC) are employed to approximate the posterior distribution, broadening the applicability of Bayesian methods in complex real-world problems.
Conclusion
Bayesian updating represents a fundamental shift from traditional frequentist approaches, emphasizing the dynamic updating of beliefs with new evidence. Its mathematical framework and philosophical underpinnings provide a robust basis for statistical analysis in data science, offering clarity and flexibility in understanding and responding to the uncertainties of the real world.